Modeling Past Surprise in Google Titans

Nell’ambito dell’apprendimento automatico, la capacità di riconoscere e gestire gli eventi “sorprendenti” — ovvero situazioni in cui la previsione di un modello differisce in modo significativo dall’osservazione — è cruciale per garantire che il sistema si adatti efficacemente ai nuovi dati. L’algoritmo di Google Titans fa leva su questo principio introducendo una componente di “sorpresa” nel meccanismo di aggiornamento della memoria neurale. Questa memoria consente al modello di apprendere da eventi inaspettati, conservarne traccia e, allo stesso tempo, dimenticare gradualmente l’effetto di sorprese superate.

L’idea di base è trattare la “sorpresa” come un segnale di errore che misura quanto l’evidenza corrente sia distante dalle previsioni del modello. Il sistema aggiorna quindi il proprio stato interno, aumentando il peso degli eventi effettivamente sorprendenti e attenuando col passare del tempo l’influenza di quelli vecchi. Grazie a questo approccio, Google Titans è in grado di adattarsi a contesti dinamici, evitare eccessivi “scossoni” dovuti a rumore e, al contempo, ricordare a lungo termine gli eventi più significativi per il proprio apprendimento.

Adesso vediamo nel dettaglio la formula Modeling Past Surprise in Google Titans

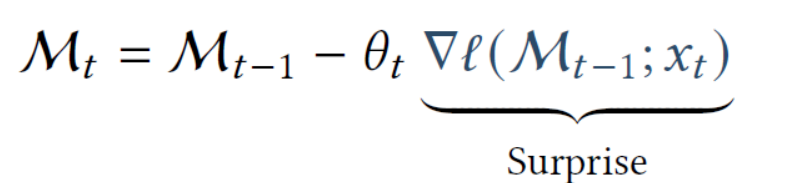
Queste formule descrivono in che modo, in un modello neurale, si tiene traccia della “sorpresa” passata e la si combina con la “sorpresa momentanea” per aggiornare una sorta di “memoria” interna MtM_t. L’idea di fondo è ispirata alla psicologia: un evento inaspettato non ci sorprende per sempre, ma lascia comunque una traccia mnemonica (il “ricordo” di quella sorpresa).

Spiegazione delle Formule

Le due principali equazioni sono:

Mt = Mt-1 + St

St = ηt   St-1  −  θt ∇ℓ(Mt-1; xt)

1. Memoria Mt

M_t rappresenta la memoria al tempo t. Essa si ottiene dalla memoria precedente M_t-1 aggiungendo il termine di sorpresa S_t:

Mt = Mt-1 + St

2. Sorpresa St

S_t racchiude la sorpresa che si manifesta al tempo t. La sorpresa si compone di una parte che tiene traccia delle sorprese precedenti (con un fattore di decadimento) e di una parte che cattura la sorpresa momentanea (il gradiente della perdita).

St = ηt St-1 − θt ∇ℓ(Mt-1; xt)

• ηt è un fattore di decadimento (spesso compreso fra 0 e 1) che regola quanto la sorpresa precedente St-1 influisca ancora sul nuovo stato.
• ∇ℓ(Mt-1; xt) è il gradiente della funzione di perdita ℓ rispetto alla “memoria” Mt-1, valutato sul dato xt. Più questo gradiente è elevato, più differisce la previsione dal valore reale osservato (maggiore è la “sorpresa” momentanea).
• θt bilancia la rilevanza della sorpresa momentanea.

3. Significato Intuitivo

Se ∇ℓ è grande, significa che il modello ha commesso un errore significativo nel predire xt; di conseguenza St aumenta e influisce maggiormente su Mt. Nel frattempo, la componente ηt St-1 mostra che la sorpresa precedente non sparisce all'istante, bensì viene “ricordata” nel nuovo valore di sorpresa St.

In questo modo, il modello conserva la memoria di eventi inaspettati, ma ne riduce gradualmente l’influenza col passare del tempo. Alla fine, Mt (la “memoria a lungo termine”) integra sia la sorpresa corrente, sia quella passata, permettendo al sistema di apprendere dagli eventi più rilevanti e di non dimenticare del tutto quelli passati.